LIMIT FUNGSI

Hollaa^^kali ini saya akan membahas materi tentang "Limit Fungsi". Kalian pasti sudah tidak asing lagi dengan kata Limit bukan? Yah, Limit merupakan salah satu pengetahuan dasar untuk memahami integral dan diferensial. Untuk itu agar lebih jelasnya yuk kita simak penjelasan dibawah ini.

A. Limit

        Apa itu limit?  Limit adalah subjek matematika yang mempelajari apa yang terjadi pada suatu fungsi ketika inputnya dimasukkan mendekati suatu angka. 

B. Limit Fungsi

  artinya nilai x mendekati nilai a (tetapi x ≠ a) maka f(x) mendekati nilai L. 

C. Sifat-Sifat Limit

1.     

2.     

3.     

4.     

5.     Jika  dan  maka: 

6.     

7.     

8.     , untuk 

9.     Jika  maka:  untuk L ≠ 0

10.  

D. Menentukan Nilai dari Suatu 

1.     Jika f(a) = k maka 

2.     Jika  maka 

3.     Jika  maka 

4.     Jika  atau bentuk tertentu  maka sederhanakan bentuk f(x) sehingga diperoleh bentuk f(a) seperti (1), (2), dan (3).

2.3. Limit Fungsi Tak Terhingga

1.     

2.      Jika pangkat tertinggi f(x) sama dengan pangkat tertinggi g(x)

3.      Jika pangkat tertinggi f(x) lebih kecil dari pangkat tertinggi g(x)

4.      Jika pangkat tertinggi f(x) lebih besar dari pangkat tertinggi g(x)

E. Limit Fungsi Aljabar

1. Limit Fungsi Aljabar Berhingga

1.     Jika f(a)=C, maka nilai 

2.     Jika , maka nilai 

3.     Jika , maka nilai  disederhanakan dulu menjadi bentuk 1, 2, atau 3

2. Limit Fungsi Aljabar Tak Terhingga

Menentukan nilai  atau :

1.     Jika n = m maka 

2.     Jika n > m maka 

3.     Jka n < m maka 

F. Limit Fungsi Trigonometri

Untuk menghitung nilai limit fungsi trigonometri digunakan rumus-rumus berikut:

1.     

2.     

3.     

4.     

Kemudian, secara umum dapat menggunakan langkah-langkah cepat seperti di bawah ini:

1.     

2.     

3.     

4.     

5.     

6.     

7.     

8.     

Jika terdapat fungsi cos maka ubahlah ke dalam bentuk sebagai berikut:

1.     cos x diubah menjadi 

2.      diubah menjadi 

Berikut adalah sifat-sifat teorema limit fungsi trigonometri lainnya:

1.     

2.     

3.    

4.    

5.     

6.     

7.     

G. Cara Penyelesaian Limit Fungsi

Nilai limit dari suatu fungsi dapat ditentukan dengan beberapa cara, antara lain:

1.     Substitusi                                                                                                                                                        Nilaidapat dicari dengan mensubstitusikan x = c ke f(x) sehingga. Penyelesaian dengan cara substitusi langsung hanya sah jika hasil akhirnya terdefinisi (tidak muncul bentuk tak tentu).

2.      Faktorisasi
Faktorisasi dilakukan jika nilai  tidak dapat dicari langsung dengan substitusi (muncul bentuk tak tentu ). Agar nilai limit tidak berupa bentuk tak tentu, maka f(x) diubah melalui faktorisasi.

3.      Perkalian dengan akar sekawan
Perkalian dengan akar sekawan dilakukan jika dalam pengerjaan limit fungsi aljabar, ditemukan bentuk akar. Dua bentuk akar dikatakan sekawan bila kedua bentuk akar itu dikalikan akan menjadi bilangan rasional.    

F. Contoh soal

1. Penyelesaian dengan Metode Subtitusi langsung

Hitunglah nilai limit setiap fungsi berikut:

2. Penyelesaian dengan Metode Memfaktorkan

Hitunglah nilai limit fungsi aljabar berikut ini:

diperoleh bentuk tak tentu maka dilakukan dengan cara memfaktorkan,

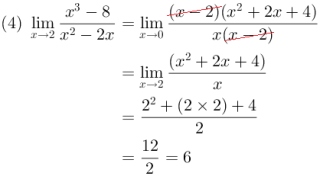
 3. Penyelesaian dengan Metode Perkalian Sekawan

Hitunglah nilai limit fungsi dibawah ini:

Diperoleh bentuk tak tentu, maka harus menggunakan cara lain yaitu mengalikan dengan akar sekawan.

Nah sampai disini dulu ya pembahasan yang dapat saya berikan kali ini. Semoga bisa bermanfaat bagi kalian semua, sampai jumpa dipembahasan berikutnya , see you next time^-^